Метод k-средних - один из самых популярных и простых методов кластеризации. Метод заключается в минимизации суммарного квадратичного отклонения точек кластеров от центров этих кластеров.
$$ V = \sum_{i=1}^{k} \sum_{x_j \in S_i} (x_j - \mu_i)^2 $$
где \(k\) — число кластеров, \(S_i\) — полученные кластеры, \(i=1,2,…,k\) и \(\mu_i\) — центры масс векторов \(x_j \in S_i\) .
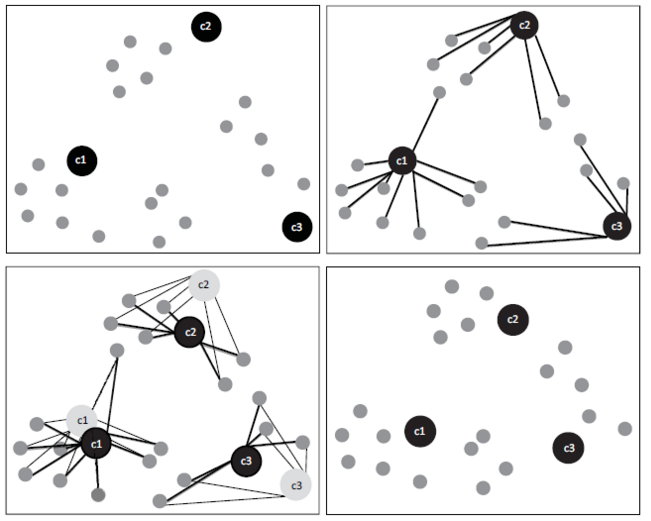
Работу этого метода замечательно демонстрирует эта картинка:
- Определяется количество кластеров и выбираются случайные начальные позиции центров кластеров.
- Для каждой точки определяется ближайшая позиция центра кластера.
- Вычисляются центроиды - центры тяжести кластеров.
- Центры кластеров перемещаются к центроидам.
- Возвращаемся к п. 2
В случае задачи обработки изображения пространством будет трехмерное пространство цветов - RGB. Поэтому точками кластеров будут являться цвета - точки пространства RGB, например (196,0,171) пурпурный цвет.
Такая задача является одной из наглядных демонстраций метода k-средних, а так же очень хорошо распараллеливается, поэтому можно решить эту задачу средствами CUDA.
Для начала нужно представить изображение в виде следующей бинарной структуры:
 Это можно сделать готовой утилитой или добавить конвертацию непосредственно в программу кластеризации.
Это можно сделать готовой утилитой или добавить конвертацию непосредственно в программу кластеризации.
Алгоритм решения примерно следующий:
Доступ к константной памяти достаточно быстрый, за счет использования кэша, но большими объемами она не располагает, поэтому в ней имеет смысл хранить лишь небольшое количество часто используемых данных. Мы имеем возможность записывать в нее данные с хоста, но при этом в пределах GPU, как и следует из названия, данные мы изменять не можем, и они доступны нам только для чтения.
Таким образом, константная память хорошо подходит для использования в алгоритме kMeans - для хранения центров кластеров, так как обращений к ним происходит достаточно много, а изменяем мы их уже на CPU. Поэтому копируем значения центров кластеров в константную память.
В ядре параллельно находим ближайшие кластеры для каждого пикселя. Если для пикселя изменился ближайший кластер, то ставим на пиксель метку о том, что необходимо продолжать итеративный процесс.
Далее на CPU обходим все пиксели, проверяя наличие меток, и вычисляя новые центры кластеров. Так как для каждого пикселя уже известен номер кластера, то находим усредненное значение всего кластера – новый центр. Если при обходе нам не встретилась ни одна метка, то это значит, что центры кластеров стабилизировались и можно завершать процесс.
У меня завалялась картинка одной модели SuicideGirls ( ͡° ͜ʖ ͡°) Возьмем ее:
Попробуем задать два кластера и обработать картинку. Два кластера - означают два усредненных цвета. Пиксели картинки прибиваются к одному из кластеров и перекрашиваются в усредненный цвет. Для двух кластеров алгоритм очень точно выделил кожу модели:
Пять, десять и тридцать кластеров соответственно:
Код решения на C\CUDA
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define BLOCK_SIZE 1024
#define MAX_GRID_SIZE 40000
#define SIZE_FILE_NAME 255
#define MAX_CLUSTERS 32
typedef unsigned char uchar;
__constant__ double3 centersDevice[MAX_CLUSTERS];
__device__ double euclideanDistance(uchar4 vec1, double3 vec2){
return pow((double)(vec1.x - vec2.x), 2) + pow((double)(vec1.y - vec2.y), 2) + pow((double)(vec1.z - vec2.z),2);
}
__global__ void kMeans(uchar4* src, int nc, int size){
int index = blockIdx.x * blockDim.x + threadIdx.x;
int offset = gridDim.x * blockDim.x;
for (int i = index; i < size; i += offset){
double min = euclideanDistance(src[i], centersDevice[0]);
int clusterNumber = 0;
for (int k = 1; k < nc; k++){
double curDst = euclideanDistance(src[i], centersDevice[k]);
if (curDst < min){
min = curDst;
clusterNumber = k;
}
}
if (src[i].w != clusterNumber){
src[i].w = clusterNumber + MAX_CLUSTERS;
}
else {
src[i].w = clusterNumber;
}
}
}
char* getline() {
char * line = (char*)malloc(SIZE_FILE_NAME);
char * linep = line;
int c;
for (;;) {
c = fgetc(stdin);
if (c == EOF)
break;
if (c == '\n')
break;
*line++ = c;
}
*line++ = '\0';
return linep;
}
int main()
{
cudaEvent_t start, stop;
cudaEventCreate(&start);
cudaEventCreate(&stop);
char* inputFileName = getline();
char* outputFileName = getline();
int nc;
scanf("%d", &nc);
int2 clusters[MAX_CLUSTERS];
double3 centers[MAX_CLUSTERS];
int w, h;
FILE *in = fopen(inputFileName, "rb");
fread(&w, sizeof(int), 1, in);
fread(&h, sizeof(int), 1, in);
int srcMem = sizeof(uchar4)* w * h;
uchar4 *src = (uchar4*)malloc(srcMem);
fread(src, sizeof(uchar4), w * h, in);
cudaEventRecord(start);
for (int i = 0; i < nc; i++){
centers[i].x = 255/nc * i;
centers[i].y = 255/nc * i;
centers[i].z = 255/nc * i;
}
uchar4 *srcDevice;
cudaMalloc((void**)&srcDevice, srcMem);
int iterations = 0;
int clusterNumber;
bool end = false;
while (!end){
end = true;
iterations++;
cudaMemcpy(srcDevice, src, srcMem, cudaMemcpyHostToDevice);
cudaMemcpyToSymbol(centersDevice, centers, MAX_CLUSTERS * sizeof(double3));
kMeans <<< min((int)ceil((double)w*h / (double)BLOCK_SIZE), MAX_GRID_SIZE), BLOCK_SIZE >> > (srcDevice, nc, w*h);
cudaMemcpy(src, srcDevice, srcMem, cudaMemcpyDeviceToHost);
cudaMemcpyFromSymbol(centers, centersDevice, sizeof(double3)* MAX_CLUSTERS);
double sumR[MAX_CLUSTERS];
double sumG[MAX_CLUSTERS];
double sumB[MAX_CLUSTERS];
double size[MAX_CLUSTERS];
for (int i = 0; i < nc; i++){
sumR[i] = 0;
sumG[i] = 0;
sumB[i] = 0;
size[i] = 0;
}
for (int i = 0; i < h; i++){
for (int j = 0; j < w; j++){
if (src[i*w + j].w >= MAX_CLUSTERS){
end = false;
src[i*w + j].w -= MAX_CLUSTERS;
}
clusterNumber = src[i*w + j].w;
size[clusterNumber] += 1;
sumR[clusterNumber] += src[i*w + j].x;
sumG[clusterNumber] += src[i*w + j].y;
sumB[clusterNumber] += src[i*w + j].z;
}
for (int i = 0; i < nc; i++){
centers[i].x = sumR[i] / size[i];
centers[i].y = sumG[i] / size[i];
centers[i].z = sumB[i] / size[i];
}
}
}
cudaEventRecord(stop);
cudaEventSynchronize(stop);
float milliseconds = 0;
cudaEventElapsedTime(&milliseconds, start, stop);
printf("Time: %f ms\n", milliseconds);
printf("Iterations: %d\n", iterations);
for (int i = 0; i < h; i++){
for (int j = 0; j < w; j++){
src[i*w + j].x = ceil(centers[src[i*w + j].w].x);
src[i*w + j].y = ceil(centers[src[i*w + j].w].y);
src[i*w + j].z = ceil(centers[src[i*w + j].w].z);
}
}
FILE *out = fopen(outputFileName, "wb");
fwrite(&w, sizeof(int), 1, out);
fwrite(&h, sizeof(int), 1, out);
fwrite(src, sizeof(uchar4), h*w, out);
}